Обрабатываемые поверхности деталей машин
В элементарной геометрии поверхность определяется как граница тела. Разглядывая границу тела разных подробностей автомобилей, нетрудно убедиться, что она состоит, в большинстве случаев, из отдельных участков, воображающих собой геометрически верные поверхности.
В будущем, говоря об обрабатываемой поверхности, мы будем иметь в виду отдельные участки неспециализированной поверхности подробности, подвергающиеся механической обработке.
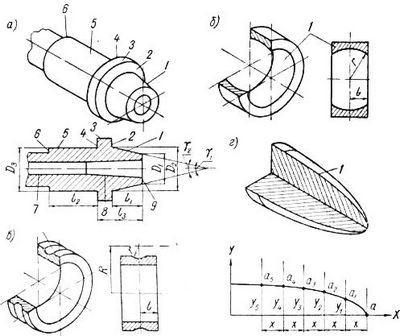
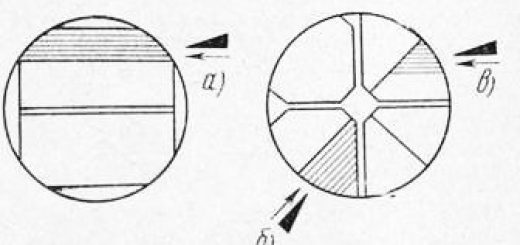
Рис. 1. Характерные обрабатываемые поверхности подробностей автомобилей типа тел вращения.
Виды поверхностей. Имеется последовательность классификаций поверхностей. Для рассмотрения способов образования поверхностей при обработке на металлорежущих станках представляется целесообразным разбить их на следующие виды: поверхности вращения, плоскости, контурно-сложные линейчатые поверхности, винтовые поверхности и пространственно-сложные поверхности.
К числу поверхностей вращения относятся: наружные и внутренние цилиндрические поверхности; конические поверхности; торцовые поверхности; сферические поверхности; тороидные поверхности поверхности с криволинейной образующей.
Рис. 2. Характерные обрабатываемые поверхности корпусных подробностей автомобилей.
К плоским поверхностям относятся поверхности, поверхности. Совокупность поверхностей типа 3 и 4 возможно названа многогранной поверхностью.
На рис. 3 представлен последовательность контурно-сложных линейчатых поверхностей. Контурно-сложной линейчатой поверхностью есть поверхность разных дисковых и плоских кулачков, поверхность некоторых видов лопаток турбин, поверхность зубьев прямозубых цилиндрических колес и ряд других.
Рис. 3. Характерные контурно-сложные обрабатываемые поверхности подробностей автомобилей.
Существенно распространены в машиностроении винтовые поверхности. Винтовые поверхности образуют витки резьбы разных винтов, червяков, цилиндрических шестерен с косым зубом.
В ряде отраслей машиностроения мы сталкиваемся с пространственно-сложными поверхностями. Такие поверхности свойственны для разных пресс-форм, штампов, некоторых видов лопаток турбин и др.
Геометрия образования поверхностей. Последовательность геометрических поверхностей возможно взят как след перемещения образующей линии по направляющей линии.
К числу таких поверхностей относятся поверхности, входящие в первые четыре группы.
Рис. 4. Пространственно-сложная поверхность.
Поверхности вращения смогут быть взяты перемещением образующей линии той либо другой формы, расположенной в осевой плоскости, по круговой линии, которая есть направляющей.
Рис. 5. Образование поверхностей.
Контурно-сложная линейчатая поверхность возможно взята при перемещении образующей линии, остающейся параллельной собственному начальному положению, на протяжении направляющей прямой линии. В случае если образующая линия имеет форму прямой, то при ее перемещении образуется плоскость.
Контурно-сложная линейчатая поверхность возможно кроме этого взята при перемещении прямой линии, которая в этом случае есть образующей, по линии, имеющей ту либо иную форму, которая в этом случае помогает направляющей. Наряду с этим прямолинейная образующая должна быть перпендикулярной к плоскости, в которой расположена направляющая линия.
Поверхности, полученные так, именуются в аналитической геометрии цилиндрическими поверхностями.
Разглядывая процесс образования поверхностей, мы предполагали, что при образовании поверхностей вращения образующая линия находится в осевой плоскости а при образовании контурно-сложных линейчатых поверхностей — в плоскости ABCD, перпендикулярной к направляющей линии. Но при образовании поверхностей в ходе обработки на станках образующая линия может занимать и иное положение.
К примеру, при образовании поверхностей вращения она возможно находится в плоскости A BCD, параллельной осевой плоскости. Предположим, что образующая есть прямолинейной и наклонена под углом в плоскости ABCD.
Разглядим вопрос о форме образующей линии, расположенной в осевой плоскости, которую будем именовать настоящей образующей линией, в отличие от образующей, которую назовем создающей образующей линией.
Как видно из уравнения, настоящая образующая уже не есть прямой линией. Величина отклонения настоящей образующей от прямой зависит от смещения х0.
Во многих случаях это отклонение не выходит из пределов, допустимых требованиями к точности обработки.
Подобная же картина получается при обработке линейчатых поверхностей. Располагая образующую в плоскости ABCD, не перпендикулярной к направляющей, мы возьмём искажение настоящей образующей.
К примеру, при образующей в форме дуги окружности настоящая образующая будет дугой эллипса.
Вопрос об искажении настоящей образующей детально рассматривается в курсе проектирования режущего инструмента в разделе, посвященном фасонному инструменту. Но данный вопрос имеет значительное значение и при вторых способах обработки, исходя из этого при оценке точности получающихся поверхностей нужно уделять внимание вопросам верного размещения образующей линии в соответствии с принятым процессом образования поверхности, определяя величину получающихся отклонений на базе соответствующих расчетов.
При обработке сферических поверхностей должен быть задан радиус г и величина I, определяющая положение центра образующей на протяжении оси. При обработке тороидных поверхностей нужно, помимо этого, задать радиус R.
При образовании поверхностей вращения разного рода корпусных подробностей должны быть кроме этого заданы координаты оси обрабатываемой поверхности х0 и у0, х1 и у1 и т. д.
Для фасонных поверхностей вращения должна быть известна форма профиля образующей линии. Образующая линия возможно алгебраической и тогда ее возможно задать уравнением либо кривой, выстроенной на базе тех либо иных эмпирических данных.
В последнем случае профиль задается координатами последовательности точек профиля а—ап, забранных с определенными промежутками х. Эти координаты именуются координатами опорных точек профиля.
Задание профиля кривой уравнением имеет суть в том случае, в то время, когда конструкция станка разрешает воспроизвести форму образующей конкретно методом соответствующей настройки станка, в другом случае на базе уравнения определяются координаты опорных точек профиля.
При обработке плоскостей нужно кроме этого задать координаты, определяющие положение этих плоскостей довольно тех либо иных баз. К примеру, положение плоскости определяется координатой z, плоскости — координатой у. Для плоскостей, расположенных под углом , должны быть, помимо этого, заданы углы наклона ух, у2, и размеры, определяющие положение их довольно базисных поверхностей.
Так, размер а всецело определяет положение поверхности довольно базисной поверхности, а размер b — длину наклонной образующей.
При обработке винтовых поверхностей нужно задать профиль образующей, внутренний Dx и наружный D2 диаметры винтовой поверхности и ход t.
При образовании контурно-сложных линейчатых поверхностей перемещением прямолинейной образующей по криволинейной направляющей профиль направляющей задается или уравнением, или координатами опорных точек. В полярной совокупности координат задаются радиусы векторы q—Qn точек а—ап, расположенных с промежутками у.
Пространственно-сложные поверхности также будут быть заданы уравнениями либо координатами опорных точек. При задании поверхности координатами опорных точек берется последовательность сечений п1 — пх, пп — п, расположенных с промежутками у, и для каждого сечения задаются координаты опорных точек кривых, получающихся в следствии пересечения поверхности с секущей плоскостью.