Рекорд с чистого листа: бумага сдаётся 12 раз
Нам так и не удалось отыскать источник этого обширно распространённого поверья: ни один лист бумаги нельзя сложить в два раза больше семи (по некоторым данным — восьми) раз. В это же время текущий рекорд складывания – 12 раз.
И что необычнее, в собственности он девушке, математически обосновавшей эту «тайную бумажного страницы».
Очевидно, мы говорим о бумаге настоящей, имеющей конечную, а не нулевую, толщину. В случае если складывать её бережно и до конца, кроме разрывы (это крайне важно), то «отказ» складываться в два раза обнаруживается, в большинстве случаев, уже по окончании шестого раза. Реже – седьмого.
Попытайтесь выполнить это с листком из тетради.
И, как ни необычно, от его толщины и размеров листа ограничение мало зависит. Другими словами, просто так забрать узкий лист побольше, да и сложить его в два раза, раз допустим 30 либо хотя бы 15 – не получается, как ни бейся.
В популярных подборках, типа «А понимаете ли вы что…» либо «Необычное рядом», факт этот — что вот больше как раз 8 раз сложить бумагу запрещено — до сих пор возможно отыскать весьма во многих местах, в Сети и вне. Но факт ли это?
Позволяйте рассуждать. Каждое сложение удваивает толщину кипы. В случае если толщину бумаги принять равной 0,1 миллиметра (размер страницы мы на данный момент не разглядываем), то сложение её в два раза «всего» 51 раз даст толщину сложенной пачки в 226 миллионов километров.
Что уже очевидный вздор.
Мировая рекордсменка Бритни Гэлливан и бумажная лента, сложенная в два раза (в одном направлении) 11 раз (фото с сайта mathworld.wolfram.com).
Думается, тут-то мы начинаем осознавать, откуда берётся известное многим ограничение на 7 либо 8 раз (ещё раз – бумага у нас настоящая, она не тянется до бесконечности и не рвётся, а порвётся – это уже не складывание). И однако…
В 2001 году одна американская школьница решила близко заняться проблемой двойного складывания, а оказалось из этого целое научное изучение, да ещё и всемирный рекорд.
Фактически, началось всё с вызова, кинутого педагогом ученикам: «А вот попытайтесь сложить хоть что-нибудь пополам 12 раз!». Дескать, убедитесь, что это из разряда совсем неосуществимого.
Бритни Гэлливан (Britney Gallivan) (увидим, на данный момент она уже студентка) сначала отреагировала как Алиса Льюиса Кэрролла: «Безтолку и пробовать». Но так как сказала Алисе Королева: «Осмелюсь заявить, что у вас не было громадной практики».
Вот Гэлливан и занялась практикой. Порядком намучившись с различными предметами, она сложила-таки лист золотой фольги в два раза 12 раз, чем посрамила собственного учителя.
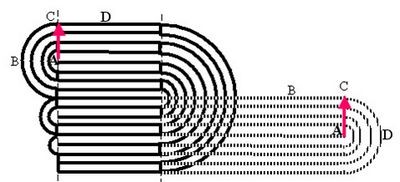
Пример складывания страницы в два раза четыре раза.
Пунктир – прошлое положение трёхкратного сложения. Буквы говорят о том, что точки на поверхности страницы смещаются (другими словами, страницы скользят относительно друг друга), и занимают в следствии не то положение, как может показаться при беглом взоре (иллюстрация с сайта pomonahistorical.org).
На этом женщина не успокоилась. В декабре 2001 года она создала математическую теорию (ну, либо математическое обоснование) процесса двойного складывания, а в январе 2002 года проделала 12-кратное складывание пополам с бумагой, применяя последовательность правил и пара направлений складывания (для любителей математики, пара подробнее — тут).
Бритни увидела, что к данной проблеме ранее уже обращались математики, но верного и проверенного практикой ответа задачи ещё никто не предоставлял.
Гэлливан стала первым человеком, что верно осознал и обосновал обстоятельство ограничений на сложение. Она изучила накапливающиеся при складывании настоящего страницы эффекты и «утрату» бумаги (да и любого иного материала) на сам сгиб.
Она взяла уравнения для предела складывания, для любых исходных параметров страницы. Вот они.
Первое уравнение относится к складыванию полосы лишь в одном направлении. L — минимально вероятная протяженность материала, t – толщина страницы, и n — число выполненных сгибов вдвое.
Очевидно, L и t должны быть выражены в одних и тех же единицах.
Гэлливан и её рекорд (фото с сайта pomonahistorical.org).
Во втором уравнении речь заходит о складывании в разных, переменных, направлениях (но всё равняется – в два раза любой раз). Тут W – ширина квадратного страницы.
Правильное уравнение для складывания в «других» направлениях – более сложное, но тут приводится форма, дающая весьма близкий к действительности итог.
Для бумаги, которая не есть квадратом, вышеупомянутое уравнение всё ещё даёт очень правильный предел. В случае если бумага, скажем, имеет пропорции 2 к 1 (по длине и ширине), легко сообразить, что необходимо сложить её один раз и «привести» к квадрату двойной толщины, а после этого воспользоваться упомянутой выше формулой, в мыслях держа в уме одно лишнее складывание.
В собственной работе школьница выяснила строгие правила двойного сложения. К примеру, у страницы, что свёрнут n раз, 2n неповторимых слоёв обязаны лежать подряд на одной линии.
Секции страницы, не удовлетворяющие этому критерию, не смогут принимать во внимание как часть свёрнутой пачки.
Так вот Бритни и стала первым в мире человеком, сложившим лист бумаги в два раза 9, 10, 11 и 12 раз. Возможно сообщить, не без помощи математики.



