Мистические задачи леонардо фибоначчи
Отечественный читатель из Волгодонска Андрей Никитин исследует совокупности Ф-счета. Он уверен в том, что простота предложенного им счётного процесса и появляющаяся симметрия чисел разрешит осознать правила устройства мироздания.
В базе Ф-счёта лежит иррациональное число Ф=1,618…, в противном случае именуемое «золотое сечение» либо «божественная пропорция» и связанное с последовательностью Фибоначчи.
Согласно точки зрения Андрея Никитина, число Ф владеет какой-то необычной неуловимостью. Оно появляется в разных проекциях, так и не давая ответа на вопрос, как это число связано с тем либо иным явлением. Интерес к мистическому числу Ф достаточно периодичен.
Он появляется с обнаружением нового проявления этого числа в каком-либо явлении природы.
Проходит время, и интерес к нему спадает. Но ненадолго.
Числу Ф находят новое и всё новое использование, но оно так и остается недоступным для ясного и полного понимания его степени и свойств его влияния на окружающий мир.
В базе счёта лежат простые числа 1,2,3… Нам известны разные совокупности счёта: древнегреческая, римская, арабская и без того потом.
А с возникновением компьютеров — ещё и бинарная, бинарно-десятичная, восьмеричная, шестнадцатеричная… Вычислять возможно по-различному, но время от времени ответственнее сам счёт, чем итог.
Нужно ли изобретать новую? Совокупность Ф-счёта разрешила по-новому посмотреть на организацию счёта и счётный процесс.
Другой принцип счёта даёт новые возможности.
На правилах Ф-счёта выяснилось вероятным моделирование числового канала и числового генератора передачи. Появились термины — числовая числовые цепи и обратная связь. И выяснилось серьёзным, в какую сторону складывать и какие конкретно единицы.
Понятия «симметричный» и «периодический» счёт приобрели новое обоснование.
Математик Макс Коен, киногерой Даррена Аранофски «Пи», уверен в том, что последовательность Фибоначчи и число Пи — это ключ к мирозданию.
Простота счётного процесса и появляющаяся симметрия чисел разрешает думать о широком применении правил Ф-счёта в окружающем мире. Как «вычисляют» растения? На каких правилах счёта трудится мозг?
Быть может, на правилах Ф-счета.
Предложенные Андреем формулы даны, по его собственному признанию, скорее для обоснования правильности и контроля размышления тех либо иных выводов, и не должны вызывать опасений из-за собственной сложности. Тем более, что их очень мало.
Совокупность Ф-счёта имеет недостатки и свои преимущества. И собственную область применения.
Ф-счёт не имеет возможности заменить существующие совокупности счёта. У него другие возможности.
Скачать полный текст работы Андрея Никитина (с подробными комментариями и формулами) вы имеете возможность тут (ZIP-архив Word-файла 205K).
С Андреем Никитиным кроме этого возможно связаться по email nikitin@volgodonsk.ru.
От себя увидим, что так называемая последовательность Фибоначчи, вправду, есть одной из самых интригующих страниц в истории математики. Средневековый пизанский торговец-математик Леонардо Фибоначчи, создатель потерянного абака «и трактата», выяснил развитие математики в Западной Европе на пара столетий.
Как раз по этому трактату европейцы познакомились с индусскими (арабскими) цифрами.
В этом легендарном трактате Фибоначчи изложил следующую задачу:
«Некто поместил несколько кроликов в некоем месте, огороженном со всех сторон стеной, дабы определить, сколько пар кроликов родится наряду с этим в течение года, в случае если природа кроликов такова, что через месяц пара кроликов создаёт на свет другую несколько, а рождают зайцы со второго месяца по окончании собственного рождения».
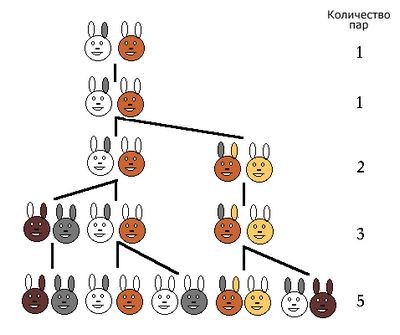
В средневековой тайной с зайцами, которую загадал Фибоначчи, кроется мистическая последовательность чисел.
Ясно, что в случае если вычислять первую несколько кроликов новорожденными, то на второй месяц мы будем как и раньше иметь одну несколько; на 3-й месяц- 1+1=2; на 4-й- 2+1=3 пары (потому что из двух имеющихся пар потомство даёт только одна пара); на 5-й месяц- 3+2=5 пар (только 2 появившиеся на 3-й месяц пары дадут потомство на 5-й месяц); на 6-й месяц- 5+3=8 пар (потому что потомство дадут лишь те пары, каковые появились на 4-м месяце) и без того потом.
Так, в случае если обозначить число пар кроликов, имеющихся на n-м месяце через Fk , то F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13, F8=21 и без того потом, причём образование этих чисел регулируется неспециализированным законом:
Fn=Fn-1+Fn-2 при всех n2, так как число пар кроликов на n-м месяце равно Fn-1 пар кроликов на предшествующем месяце плюс число снова появившихся пар, которое сходится с числом Fn-2 пар кроликов, появившихся на (n-2)-ом месяце (потому что только эти пары кроликов дают потомство).
Числа Fn , образующие последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … именуются «числами Фибоначчи», а сама последовательность — последовательностью Фибоначчи.
Сущность последовательности Фибоначчи в том, что, начиная с 1,1, следующее число получается сложением двух прошлых. Последовательность асимптотически (приближаясь всё медленнее и медленнее) пытается к некоему постоянному соотношению.
Но, это соотношение иppационально и является числом с нескончаемой, непредсказуемой последовательностью десятичных цифр в дробной части. Его нереально выразить совершенно верно.
Особенные заглавия этому соотношению начали давать ещё перед тем, как Лука Пачиоли (средневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий имеется такие, как «Золотое сечение», «Золотое сpеднее» и «Отношение веpтящихся квадpатов».
Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе пpинято его обозначение гpеческой буквой фи.
Мистический суть последовательности Фибоначчи заключён в том, что отдельные числа из суммационной последовательности Фибоначчи возможно заметить, к примеру, в перемещениях цен на товаpы. Kолебания соотношений около значения 1.618 на громадную либо меньшую величину мы обнаpужим в Волновой теоpии Эллиотта, где они описываются Пpавилом чеpедования.
Последовательность Фибоначчи — это не просто игра с числами, а самое ответственное математическое выражение природных явлений из всех когда-либо открытых.
Как раз с ней связывают универсальность существующих в природе форм. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических совокупностях, в генных структурах живых организмов.
Эти закономерности имеется в строении отдельных тела и органов человека в целом, и проявляются в функционировании и биоритмах зрительного восприятия и головного мозга.
Более того, кое-какие элементы данной последовательности соответствуют хронологическим пределам в старейшей истории , в особенности в случае если к числам добавить наименование «тысяч лет до н. э.», либо «тысяч лет тому назад», либо легко «тысяч лет».
Так, позицию 233 тысяч лет в приводимой последовательности возможно отождествить с датой рисского оледенения в Европе, общепризнанная геологическая дата которого 230 тысяч лет тому назад. Позиция, соответствующая 377 тысячам лет, близка дате в 400 тыс. лет тому назад — к этому времени относят выход человечества из биоценоза.
Последовательность Фибоначчи остаётся математической каббалой сейчас, и каждое новое открытие бросает новый отблеск на волшебство этих цифр.