Математические модели обучаемости
При организации совокупности подготовки появляется необходимость в ответе последовательности практических задач, которые связаны с прогнозированием и планированием ее результатов.
К таким задачам относятся:
— оценка вероятного уровня подготовки оператора (коллектива операторов) при заданном времени подготовки;
— прогнозирование времени, нужного для подготовки оператора до заданного уровня;
— прогнозирование затрат на подготовку;
— выбор рационального соотношения личного и коллективного этапов подготовки;
— определение допустимых перерывов между тренировками, снабжающих поддержание навыков на требуемом уровне;
— обоснование нормативов работы и т. д.
Для решения аналогичных задач нужно иметь математические модели обучаемости. Известны два метода получения таких моделей:
1) экспериментальный, заключающийся в аппроксимации экспериментальных данных, взятых в следствии анализа разных процессов подготовки, самая подходящей аналитической функцией;
2) получение аналитических зависимостей теоретическим методом на базе какой-либо известной теории, удовлетворяющей психотерапевтическому и математическому представлениям процесса подготовки.
Характерной изюминкой показавшихся в первой половине XX века математических моделей обучаемости (Щукарева, Робертсона, Тэрт-сона, Гулликсена, Халла и др.) есть их эмпирическая база. Исходным материалом для их получения помогали экспериментальные изучения, проводившиеся, в большинстве случаев, над животными.
Не обращая внимания на то, что многие выводы подтвердились и в отношении человека, существует множество качеств обучения, характерных лишь ему.
В некоторых работах обучение рассматривается с позиций внутренних процессов, происходящих в обучаемом. Авторы этих работ стремятся представить процесс^ обучения функцией многих параметров.
Примером для того чтобы подхода есть интегральный способ оценки натренированности операторов, основанный на учете всей совокупности отклонений параметров управляемого процесса, количественных значений физиологических показателей, несущих основные данные о координации работы и состоянии оператора разных совокупностей его организма, и на оценке информационных процессов в замкнутой совокупности.
Существует два подхода к изучению сложных явлений (совокупностей): макроподход и микроподход.
Макроподход не требует полного анализа исследуемой совокупности. Она в этом случае рассматривается как «тёмный ящик», внутреннее строение которого практически или полностью неизвестно.
Разглядывая совокупность, складывающуюся из бессчётных элементов, как что-то целое, при макроподходе изучают зависимость выходных параметров совокупности от сигналов на входе и ее черт без изучения процессов, происходящих в совокупности.
Микроподход предполагает, первым делом, детальное^ изучение структуры совокупности для оценки влияния процессов, происходящих внутри ее, на выходные параметры.
Непременно, самый детально совокупность возможно изучена при применении обоих подходов, каковые взаимно дополняют друг друга. Но во многих случаях возможно ограничиться одним из них.
К примеру, при анализе совокупности подготовки операторов, в то время, когда нужно распознать неспециализированные закономерности увеличения качества работы оператора по мере его подготовки, возможно воспользоваться лишь макроподходом. Ниже рассматривается вывод модели обучаемости с позиций макроподхода н базе теории информации.
Для однозначности предстоящих рассуждений направляться сразу же установить, что введение^понятия «информация» в психологию вовсе не предполагает отождествления процессов переработки человеком данных, его соответствующих процессов и восприятия в технических совокупностях. Речь заходит о приравнивании этих процессов друг другу только на определенном уровне абстракции, а именно на уровне, разрешающем их квантификацию.
Такое приравнивание нужно в первую очередь для ответа практических задач, поскольку в условиях автоматизации производственных .процессов человек реально имеет дело с информацией, предъявляемой в той особой форме, которая характерна ее техническим источникам, и входит в единую совокупность циркуляции информации. Данный подход представляется наиболее целесообразным, и в случае если направляться ему, то можно считать допустимым применение в разум-
Ных пределах аппарата теории информации к описанию процесса подготовки человека.
С позиций кибернетики человеческий организм представляет собой самая сложную динамическую совокупность, которой характерно управление с обратной связью, осуществляемое на базе переработки информации. Эта совокупность складывается из множества систем, координация которых для конкретной деятельности до начала процесса обучения выражена слабо.
С началом этого процесса происходит упорядочение связей, каковые первоначально пребывали в относительном беспорядке, устанавливается лучшая координация систем организма, в следствии чего обученные операторы более верно и с меньшей затратой энергии делают собственные функциональные обязанности.
Перевод (либо переход) совокупности в одно из вероятных для нее состояний методом действия (среди них и информационного) на ее переменные имеется не что иное, как управление. Следовательно, процесс обучения в этом случае возможно разглядывать как процесс управления.
Как мы знаем, что количество информации, накопленное в совокупности.управления (и обучения) в следствии ее информационного сотрудничества с окружающей средой, обусловливает определенный уровень организации данной совокупности. По отношению к человеку это указывает, что приобретаемая им на протяжении подготовки информация присоединяется к уже накопленной (в этом случае выступающей в качестве знаний) и влияет на его будущие действия.
Исходя из данной посылки для математической формализации процесса обучения возможно воспользоваться созданным академиком В. А. Трапезниковым математическим аппаратом, обрисовывающим кое-какие закономерности сложной управляемой совокупности. Тогда низкая приспособленность оператора к исполнению собственных обязанностей возможно растолкована, первым делом, имеющей место неупорядоченностью связей между возможно действиями и возможными операциями.
Логарифмическая сообщение между множеством и энтропией неупорядоченных состояний, принятая в теории информации и статистической физике, логична и с позиций обучения: энтропию двух последовательно трудящихся операторов конечно вычислять суммой энтро-пий каждого из них, одновременно с этим неспециализированное число неупорядоченных состояний двух операторов равняется произведению чисел их неупорядоченных состояний.
Неупорядоченность совокупности понижается введением управления, наряду с этим уменьшение неупорядоченности прямо пропорционально количеству использованной в ходе управления информации.
Зависимость качества работы оператора от количества управляющей информации представляет собой, экспоненциальную функцию.
Главная трудность применения на практике выражения содержится в необходимости оценки количества информации, в особенности с учетом ее ценности и значимости.
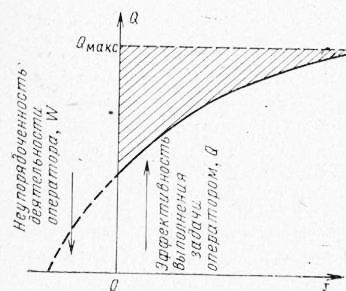
Рис. 1. Зависимость эффективности работы оператора от количества использованной им управляющей информации
Рис. 2. Зависимость эффективности работы оператора от времени обучения (количества тренировок)
Значительные различия между ними заключаются в следующем. Большая часть моделей обучаемости строится из предположения о наличии у каждого оператора собственного «потолка» в уровне подготовки, что не может быть им превзойден.
Такое утверждение не есть строгим, поскольку, в принципе, нет оснований сомневаться в том, что индивидуума, удовлетворяющего требованиям, предъявляемым к оператору данной профессии, возможно научить до нужного уровня. Целый вопрос сводится только к промежутку времени, нужному для его подготовки, и способу подготовки.
О каком-то «личном потолке» возможно сказать лишь при ограниченных сроках подготовки оператора, в то время, когда не все кандидаты из-за личных различий способны с однообразным качеством за одно да и то же время овладеть профессией. В базу уравнения положены возможности оператора с минимально достижимой неупорядоченностью деятельности, к которой, в принципе, может «приблизиться» любой кандидат, удачно прошедший соответствующий опытный отбор.
Предельные же возможности конкретных операторов рассматриваются в этом случае лишь с позиций их сравнения с вышеуказанным оператором на том либо другом этапе подготовки при всех равных условиях.
Предположение о наличии у каждого индивидуума собственного «потолка» значительно снижает практическую значимость ранее предлагавшихся моделей обучаемости, поскольку количественная оценка данной константы требует долгого периода изучения каждого кандидата раздельно. Наличие же единого для всех индивидуумов потолка разрешает перейти к одной константе, которую возможно выяснить или по итогам экспериментальных изучений, или теоретически на основании анализа качества деятельности операторов данной профессии.
Напоследок направляться подчернуть, что рассмотренная модель обучаемости воображает математическую формализацию процесса формирования навыков на базе выходных показателей, характеризующих данный процесс без раскрытия его микроструктуры.
Однако значимость указанной модели определяется тем, что она разрешает решать последовательность серьёзных практических задач, составляющих базу организации совокупности подготовки.